Union-Find and Minimum spanninng tree

Fun with Data-Structures and Graphs

Goal

Learn a Data Structure that is not in the STL.

Discover yet another graph algorithm.

Union-Find

• Problem: Find connected components in an undirected graph.
• Solution: DFS and coloring(task passports from tuesday). Runs in $\mathcal{O}(\left|V\right| + \left|E\right|)$.
• Problem: Find connected components after we add an edge to the graph.
• Solution: Use DFS every time the graph changes. Runs in $\mathcal{O}(C \cdot (|V| + |E|))$

What do we need to be more efficient?

Avoid doing DFS each time when just one edge changed.

Operations we need to be fast:

• Check wheter two islands are connected.
• Connect two islands

Idea: Use the STL

• vector<set<island>>
• set<set<island>>
• Connect two islands: $\mathcal{O}(|V| \cdot \log|V|)$
• We can do better: $\approx \mathcal{O}(1)$ for both operations

Union-Find

Definition: The Union-Find Disjoint Set is a data structure to model a collection of disjoint sets with the ability to efficently determine which set an item belongs to and to unite two disjoint set into one larger set.

Efficiency

• We want to keep the height of the trees as small as possible.
• For every item keep track of the hight the tree of its children. If we merge two, merge the smaller into the bigger. (Union by rank heuristic)
• Once we found the root, set the parent of all seen items directly to the root.
• Also called path compression heuristic.

Code

class UnionFind {
    UnionFind(int N);
    int findSet(int i);
    bool inSameSet(int i, int j);
    void unionS(int i, int j);
};

Implement the functions by yourself.

class UnionFind {
    private:
    vector<int> p, rank;
    UnionFind(int N) : rank(N), p(N) {
        for(int i = 0; i < N; i++)
            p[i] = i;
    }

    bool inSameSet(int i, int j) {
        return findSet(i) == findSet(j);
    }
};

int UnionFind::findSet(int i) {
    if(p[i] == i)
        return i;
    return p[i] = findSet(p[i]);
}

void UnionFind::unionS(int i, int j) {
    if(!inSameSet(i,j))
        return;
    int x = findSet(i), y = findSet(j);
    if(rank[x] > rank[y])
        p[y] = x;
    else {
        p[x] = y;
        if(rank[x] == rank[y])
          rank[y]++;
    }
}

Questions?

Minimum Spanning Tree

Definition: A spanning tree of a graph G=(V,E) is a subset of edges $E' \subseteq E$ forming a tree connecting all vertices of V.

Motivation

We can model a problem of building a road network in a remote villages as an MST problem. The vertices are the villages and the edge weight represent the cost of connecting those two villages. The MST of this graph represents the minimum cost road network that connects all these villages.

Example

Example

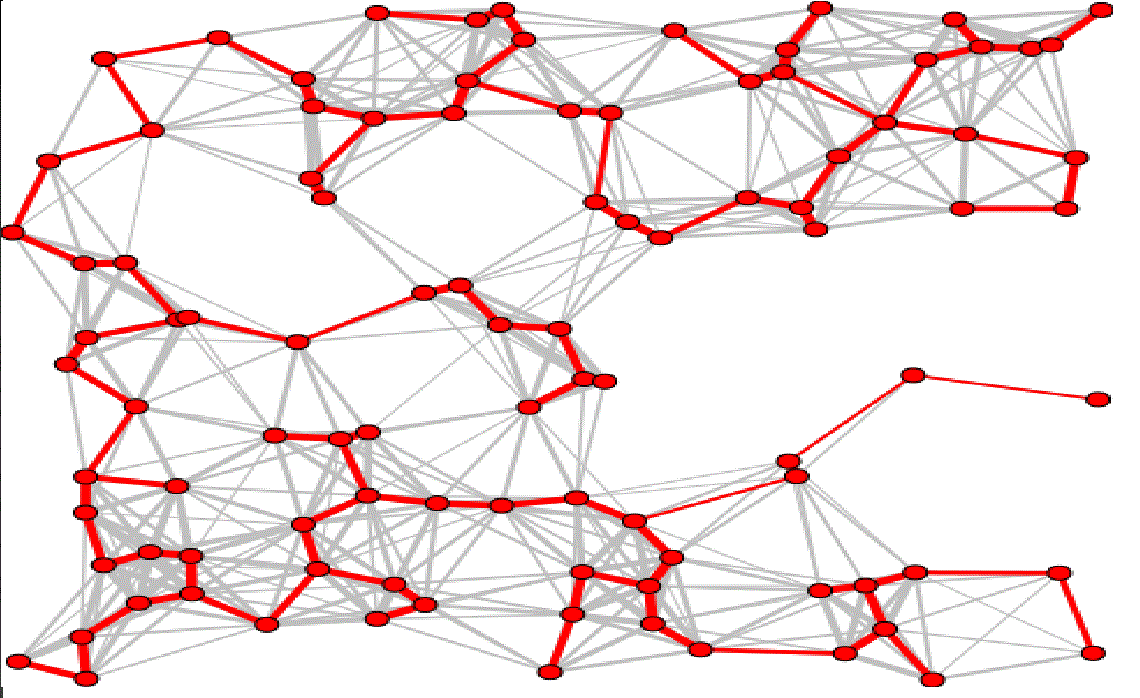
Observations

From now on we assume that the graph is connected and undirected.

• All spanning trees of an unweighted (or equally weighted) graph G are spanning trees.
• There is at least one minimum spanning tree
• A spanning tree has $|V|-1$ edges
• If each edge has distinct weight then there will be only one unique minimum spanning tree

How do we find the Minimum spanning tree?

Kruskal and Prim

Kruskal

• Sort all edges in decreasing order by weight.
• Greedily try to add each edge into the MST.
• Check that the new edge doesn't create a cycle.
• Running time: $\mathcal{O}(E \cdot \log E + E \cdot (\approx \mathcal{O}(1))) =$ $\mathcal{O}(E \cdot \log E) = \mathcal{O}(E log V)$

Code

int main() {
  vector<pair<int, edge>> edges // (weight, edge{from, to})
  sort(edges.begin(), edges.end());
  int mst_cost = 0;
  UnionFind UF(V);
  for(int i = 0; i < E; i++) {
    auto front = edges[i];
    if(!UF.inSameSet(front.second.from, front.second.to) {
      mst_cost += front.first;
      UF.unionS(front.second.from, front.second.to)
    }
  }
}

Prim

• Chose a arbitrary vertex as start graph M.

• As long as $M \subset V (M \neq V)$

  1. Chose a edge e with minimal weight that connects a vertex in M with a vertex v that is not in M.
  2. Add e and v to the graph M.
• Complexity: $\mathcal{O}(E + V \cdot \log V)$

Code

TODO

Cycle Property

Property: For any cycle C in the graph, if the weight of an edge e of C is larger than the individual weights of all other edges of C, the this edge cannot belong to a MST.

Cut Property

Definiton: A cut is a partition of the vertices of a graph into two disjoint subsets. Any cut determines a cut-set, the set of edges that have one endpoint in each subset of the partition.

Proof of Kruskal's algorithm